CuBI height | micrometeorology-en

SOFTWARE

Calculation of

Cumulative Basal Area Inflection (CuBI) height

Preface

In this page, a software of calculating cumulative basal area inflection (CuBI) height (Nakai et al., 2010) is provided.

CuBI height is the representative canopy height of a forest stand determined as the height of the inflection point of a sigmoid-shaped relationship between tree height and cumulative basal area.

Calculation of CuBI height

CuBI height is estimated from a dataset of tree height and diameter at breast height (DBH) by the following steps.

Sort tree heights of samples h(i) in ascending order.
Calculate the cumulative basal area G(i) from the shortest tree.
Plot the cumulative basal area G(i) against h(i).
Fit the following Richards function (Richards, 1959) to the data plot.

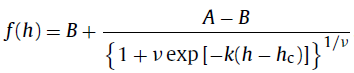
A : Upper asymptote
B : Lower asymptote
k : Shape parameter
ν : Parameter defining the non-symmetry of the curve
hc : CuBI height, inflection point of f(h)

These parameters (including CuBI height) are automatically determined by fitting f(h) to the data using a least squares method.

MATLAB program

Extract the following LZH file in the MATLAB working directory.

[CuBI_calc_MATLAB.lzh]

This archive file contains the following files.

CuBI_calc.m (Main program)
Richards.m (Richards function)
TreeData.csv (Sample tree data)

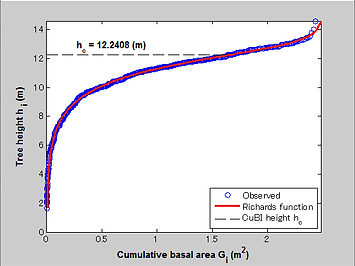
Run CuBI_calc.m, and all five parameters including CuBI height are estimated by using nlinfit function, with their 95% confidence intervals using nlparci function.

This program provides all the calculated results in CSV format, and also displays a plot as in the figure.

R program

Extract the following LZH file in the R working directory.

[CuBI_calc_R.lzh]

This archive file contains the following files.

CuBI_calc.R (Main program)
TreeData.csv (Sample tree data)

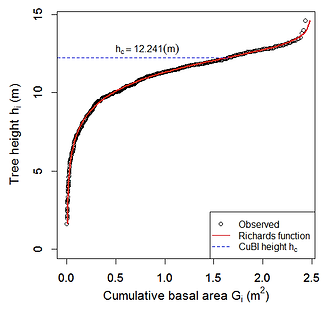
Run CuBI_calc.R, and all five parameters including CuBI height are estimated by using nls function, with their 95% confidence intervals using confint function.

This program provides all the calculated results in the TXT file, and also displays a plot as in the figure.

A Step-by-step Usage Instruction of CuBI_calc.R

Set the working directory to which the archived file was extracted. (Need instructions? See this page.)
Type source("CuBI_calc.R") [Enter] to run this program.
If an error occurred, please edit CuBI_calc.R file and try to change the nu0 value.
- The ν in the Richards function can take a large value when the sigmoid shape of the plot is significantly asymmetric. In that case, the initial value nu0 should be large to find the solution.

References

Nakai, T., Sumida, A., Kodama, Y., Hara, T., Ohta, T. A comparison between various definitions of forest stand height and aerodynamic canopy height. Agric. For. Meteorol., 150, 1225–1233, 2010.
[doi: 10.1016/j.agrformet.2010.05.005]
Richards, F.J. A flexible growth function for empirical use. J. Exp. Bot., 10, 290–300, 1959.
[doi: 10.1093/jxb/10.2.290]